0%

(2013) Auto-Encoding Variational Bayes

Posted on In , ,

Kingma D P, Welling M. Auto-encoding variational bayes[J]. arXiv preprint arXiv:1312.6114, 2013.

(Figure 1) 由于通过(可观察的)变量X推断(不可观察) latent variables比较困难 (即后验概率分布p(z|x))，论文提出VAE (变分自编码器，variational auto-encoder)结构以及AEVB (自编码变分贝叶斯)算法，即通过SGVB (随机梯度变分贝叶斯，Stochastic Gradient Variational Bayes)估计使得构造的q(z|x)分布近似难以计算的p(z|x)分布。



1. Contribution

  • 通过reparameterization方法确保梯度能够回传。
  • 通过下界估计(变分贝叶斯推导得出)近似后验概率分布。

2. 知识点延伸

  • 相对熵D(P||Q)=交叉熵H(P, Q) - 熵H(Q).
  • 熵：真实分布P的平均编码长度(大于等于0)。
  • 交叉熵：非真实分布Q的平均编码长度(大于等于[熵])。
  • 相对熵：[交叉熵]与[熵]的差，即多出的编码bit数(大于等于0)。
  1. D(Q||P)优化结果：P(绿色)尽可能包含Q.
  2. D(P||Q)优化结果：P(绿色)尽可能包含Q.


  • 变分法：推导得出泛函存在极值的必要条件：欧拉-拉格朗日方程。
  • 平均场定理：利用概率模型Q(x1, x2, …, xn)=Q(x1)Q(x2)…Q(xn)近似所要求的概率模型P(x1, x2, …, xn)=P(x1)P(x2|x1)P(x3|x2, x1)…P(xn|xn-1, …, x1).
  • 变分贝叶斯：结合平均场定理和变分法，求出近似P分布的Q分布。通过最小化目标函数KL(Q||P)，推导出最大化下界估计。利用平均场定理进一步推出需要满足


即



涉及到计算期望: 链接

3. SGVB

  • 基于变分贝叶斯推导得出的下界估计，利用平均场定理推出最终需要满足的条件(涉及到期望计算)，但分析期望相关的解仍然存在困难。

  • 因此，论文通过reparameterization方法 (而非平均场定理) 简化下界估计，公式右边两项分别通过decoder和encoder计算得出。



  • 同时，reparameterization能够使得下界估计可导 (即梯度能够回传)。

4. The Problem Scenario

  • Intractability. 边缘似然p(x)=∫p(z)p(x|z)dz难以计算，导致真实后验概率分布p(z|x)=p(x|z)p(z)/p(x)难以计算(无法使用EM算法)，以及mean-field VB难以计算。另一方面，p(x|z)可通过神经网络非线性解决。
  • Minibatch训练时，使用Monte Carlo EM非常慢。

论文旨在解决以下3点困难:

  1. 近似参数θ.
  2. 近似posterior p(z|x).
  3. 近似marginal p(x).

即引入encoder q(z|x)近似p(z|x).

  • encoder (构造概率分布φ): q(z|x).
  • decoder (真实概率分布θ): p(x|z).

论文提出一种方法联合训练encoder参数φ和decoder参数θ.

5. The Variational Bound

  • 根据VB可得到公式 (1)



  • L即为变分下界，可写成公式 (2,3)




  • (公式3) 右边两项分别为q分布与真实分布p的差异、根据z重构x的误差。

6. SGVB estimator和AEVB algorithm

  • 假设一个近似后验概率分布q(z|x)，当不假定条件x时，同样能应用于q(z)。
  • 使用包含 (auxiliary) noise variable ε的可导变换g表示random variable z (公式4)


  • 因此可以构造关于包含z~q(z|x)的函数f的Monte Carlo期望估计 (公式5)：


  • (公式2) 可改写为 (公式6)



  • 考虑到分布近似误差和重构误差，(公式2) 也可改写为 (公式7)


  • 考虑到minibatches训练，可进一步改写为 (公式8)



7. The Reparameterization Trick

假设z服从高斯分布



可写成合理形式




即



8. Example

  • 假设z的先验分布服从标准正态分布



9. Experiments

  • 增加latent variable维数不会导致过拟合。
  • y: loss, x: iteration.


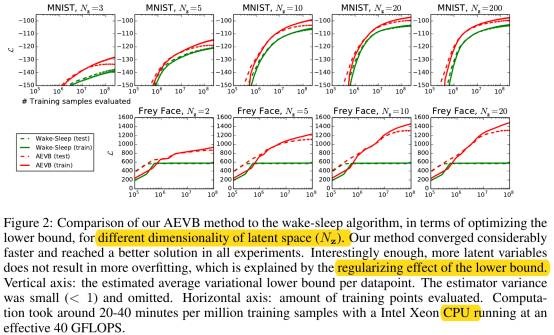
10. Solution of -D(q||p), Gaussian Case



11. MLP’s as probabilistic encoders and decoders

  • MLP (Multi-layer Perceptron)：神经网络。
  • encoder使用MLP with Gaussian output.
  • decoder使用MLPs with Gaussian or Bernoulli outputs, depending on the type of data.
  • Bernoulli


  • Gaussian